Dr. Deborah Ball: Knowing and Using Mathematics in Teaching

BALL: I'm actually very honored to be speaking with you today. There are many people in this audience whose ideas have influenced my own and from whom I've learned, and many whom have shared my interest in the problem that I'll be talking about today.

A couple of things that might help to mute Joyce's grand introduction of me is that some of you know that when I became an elementary school teacher in 1974, which is longer ago now. I'm sort of embarrassed to realize that at this point, or maybe proud. I became an elementary school classroom teacher with having taken virtually no science and no mathematics. And the reason to mention that at this point is that my interest in the topic I'll be talking about today and that concerns so many of us grows directly out of my own experience of teaching children.

That is having become a classroom teacher without that background, it quickly became apparent to me that the question of how I needed to know those two subjects in order to teach young people well was a really interesting question. And the roots of what has grown to be an interesting and vibrant research program and teaching challenge grew out of my own early efforts to remediate in some sense the fact that when you go to high school in the early 1970's you were allowed to take, basically, anything you wanted.

So I took lots of foreign language, and lots of humanities, and later on found out that maybe it was a bit of a mistake to not have opted into more math and more science. My own history in trying to learn those subjects and to learn them for teaching, which is the topic of my talk today, is what animates my current work.

The work I'll be talking about is, as Joyce said, the work of many people, among them Hyman Bass, Heather Hill, Laurie Sleep, who's here with us today, Geoffrey Phelps and Mark Thames. And I say that in part because this problem of what we really do mean by content knowledge for teaching is tough enough and complicated enough that it's a lot within a parenthesis. It's a lot more than something to just say, oh, yes, and teachers need to know their subject. It's a very tough question, or I wouldn't have been working it for the last 31 years; and it requires a lot more than an experienced classroom teacher, or a research mathematician, or people who have the kinds of background that the others in our team have. It's a complicated question and one that we're still seeking answers for.

Given the time, I'm just going to show you what kinds of things I had in mind. I will post the slides from my talk -- although I won't do all of it at this point, I will post them so that you can have them.

I wanted to say a couple of things about the policy context, because when I began to work on the question of what do teachers need to know about content, the policy pressures on that question were less than they are today; and I think the reason that the policy pressures are so great is an important additional incentive for working on this further. I will spend time on what we have come to understand about what we would call "mathematical knowledge for teaching" to update you on the progress of our theoretical work. I will also talk just a little bit about our work on developing the measures of mathematical knowledge for teaching to which Joyce referred.

And at the end, I think the link between me and Phil will help us to consider the question of how might the work that has gone on in mathematics inform or intersect with the work that those of you who focus more on science are doing on parallel questions.

So let me start into this, and we will do some of it but not all of it. I think the policy context to which you heard both of the previous speakers, Dr. Thompson and Dr. Johnson refer, is important to bear in mind. And I chose these two graphics on purpose to highlight the situation in which we we find ourselves currently. On one hand, we know very well this legislation, No Child Left Behind. This is legislation that asks us as its slogan, stated so clearly, to care more than we have before about the fact that our educational system is leaving massive numbers of students behind, and it's not random who is being left behind. This matters enormously.

So that we need new and concerted efforts to make sure that the promise and the myths, in some sense, or the dreams, let's say, of American education can be realized. So who could argue with the idea that what we need is an educational system, as Dr. Johnson just said, that would actually be able to produce students who are proficient in mathematics and science. No one can argue with that. I think our arguments come in recognizing our own lack of capacity as a nation to meet that challenge. And that, I think, is part of the reason we're all in the room today.

The competing image on this slide is perhaps less well known to you. It's the cover of a book by a professor at Stanford University, David Labaree called, "The Trouble with Ed Schools." As the new dean of an education school I am painfully aware of the fact that we're not held in high repute. We're not thought to have much to contribute to this policy question or the serious moral problem that as a nation we don't educate our young people well. And I take that as a challenge that I and my colleagues of various kinds, who work in professional education, understand that we have a job to do, and we can't do it alone. We have to do it together with others of you in this room.

It can't be the case that the challenges that the education profession faces right now can be answered by just any random person who thinks they have an idea. The questions are tough enough and important enough that we need to step up to the challenge of saying, we have ideas; they're more than our opinion. We can give evidence for the sorts of things that will make a difference for student learning.

So I think that means that our challenges include the following, those of us who consider ourselves ed. school types or classroom teachers, or people in professional education, as well as those of you who come out of the disciplines directly and who have devoted your energies to the problems of mathematics and science education. First, we have an obligation to meet the challenge of articulating more clearly what is, in fact, meant by high quality teaching. And we can't stop at that, because if that's all we talk about, we've completely missed the point. There won't be any high quality instruction in American classrooms unless we persevere and answer a second question: what does high quality teaching demand of the classroom teachers who have to produce it? And that is a non-trivial question not answerable by curriculum development, not answerable by assessments, and not answerable by lots of rhetoric about highly qualified teachers. This is a serious question, and it demands the attention of all of us in this room.

We need to find evidence for the effects of the things we consider to be high quality teaching. So we were challenged by Dr. Johnson for what are the five elements of high quality mathematics instruction. That doesn't mean that we should just make such a list. We should seek out what research we have on that and what research we yet need in order to be able to understand the components of high quality mathematics instruction. And we need what I would call rigorously and relevantly warranted professional knowledge; and by that I mean it needs to be demonstrably supported by evidence, and it has to be mathematical and scientific knowledge that is directly related to the work of teaching.

We're not interested at this point and time, nor can we afford to be interested, in simply producing a cadre of American teachers who meet some standard that somebody thinks sounds good or sounds impressive. We need our nation's teachers -- they deserve to have from those of us who have put them with professional knowledge, the kind of knowledge that makes a difference for hearing a student's idea, coming up with the right example, testing a student appropriately, explaining something in a third way when the first two haven't worked. And that is not, as Joyce said, the same kind of knowledge of science and math that people that use mathematics and science for other purposes, like doing research in those fields-- many of you in the room do that-- or people who work in physics, or biology, or accounting, or tailoring, or the number of fields that require mathematics, for example.

The knowledge that teachers need for mathematics is rigorous, typical-- and in a moment, you'll have a chance to step up to the line on that-- and is not the same. And therefore, we need ways to think about what is it that's relevant to the work of teaching and will at the same time be persuasive to those stakeholders in our society who are demanding more from our schools, as they should. We'll need answers that work both inside the classroom and in the broader policy context.

So let me talk now a little bit about what we mean by mathematical knowledge for teaching. This phrase sounds kind of like everyday language, and anybody might use it, but I and my colleagues mean something particular by this. And let me try to say why we think about it the way we do. Although many people are concerned about the fact that many teachers seem to have lacked the kind of math and science knowledge that they need for teaching, and there are plenty of reasons to point to how we know that, many of the policy solutions that people come up with, or the opinions that people hold are actually likely not to make very much difference in this problem.

For example, it's a logical thing to say that teachers should take more coursework. Well, yes, of course. But on the other hand, if we don't know what those courses ought to convey or what they ought to help people learn, we're no where. So simply adding course numbers won't help much.

Another popular solution that again makes a certain kind of sense, but by itself won't accomplish anything, is recruiting more people into teaching. Of course we need to recruit more different, more diverse people into to teaching. But again, people who happen to have devoted part of their career to working as engineers or working in other spheres where they are themselves mathematically skillful, may find it pretty difficult to figure out how to explain what an even number is to a third grader; and that's not pedagogy. That's actually something about the way you have to know the content. So recruitment alone, while laudable, won't accomplish very much.

So I want to clarify what the problem really is around teacher content knowledge. It's pretty easy to pass by it and say, yes, we agree on that. Now, what else has to happen in districts? Or what else has to be done? I want to pause on that point. So, just to remind you, in the end we're not interested in having better educated teachers really. I mean, that's great. But what we're really interested in is improving the quality of teaching and learning in mathematics and science. And from here on out, I'm mostly going to talk about math, and leave it to Phil to stretch this out to science. But those of you in the room who work on science, try to think about where the argument or the evidence I'll be showing fits and does not fit with your area.

Now, the reason to worry about teachers' knowledge of math is that teachers' ability to both use mathematics and apply it to the work of teaching matters enormously for the quality of the instruction that they can produce. So therefore, the question that we should be asking as a community is not how much mathematics or science do teachers need to know, but what question that's not so quantitative. In what way do teachers need to know mathematics? What sorts of mathematical skills does one have to use to teach mathematics? Again, I'll try to keep reminding you throughout my remarks that I'm not talking about approaches to instruction; I'm talking about how you have to think mathematically if what you do is teach it.

So, given that, the way that I and my colleagues have worked on this question-- and I should add, through generous funding from both the National Science Foundation and the Department of Ed., over 20 years really-- this is a programmatic piece of work that we still feel that we have a lot yet to do. We began by studying instruction itself. Rather than looking to standards or what experts in the field might like kids to know, we began bottom up, by looking at what goes on inside of a math classroom when teachers are engaged with the sorts of things I've been mentioning, figuring out why a student is making a mistake; choosing a good example; modifying the textbook.

And we tried to understand, as we studied classroom teaching, what are the mathematical challenges that teachers face? As we identified what some of those are, we analyzed those to ask ourselves the question, if you have to do something like choose just the right example to engage students in figuring out a new topic, what is the mathematical reasoning you have to do to choose that? And how might you have to know the topic in order to choose the example well? So that's what I mean by a practiced-based approach to answering this question.

So, let me say something about what we mean by the phrase, just so that you're clear when I said we mean it in a special way. When we say, mathematical knowledge for teaching, we mean, as I've been hinting at, the mathematical knowledge, but also the skills, habits of mind, dispositions, mathematical dispositions, mathematical skills that are entailed by the work that you do when you teach kids mathematics. And when I say the work of teaching, I don't just mean looking in the textbook, or writing a quiz, or giving an explanation. I also mean all the things that classroom teachers do that I did for years, like talk to a parent about why that parent's child is having difficulty with long division. That means you might have to help the parent know how long division needs to be understood. And that's a different challenge than talking to a third grader, and it's also a kind of knowledge that teachers need. So mathematics gets used by teachers in their classrooms and also beyond. So enough of that already. You need a chance to try this out yourself.

I'm going to go through a couple of examples where I'm going to try persuade you, if you aren't already, that the difference between knowing math yourself and knowing it for teaching is wide. So, some of you will do well on these tests, and some of you won't, and that's exactly the point. And it will be quite interesting to know what kind of expertise goes into doing well on these. In each case, I'm going to ask you to do a straight piece of math, and then I'm going to turn it a little bit to show you what you would have to do with that same piece of mathematics if what you were going to do is teach it.

So the first task for you-- here we are after lunch-- is to multiple 49 times 25. I don't care how you do it, just get an answer to it. You can compare answers if you're feeling uneasy. (laughter) Okay. Can somebody tell me what answer they got?

AUDIENCE MEMBER: 1,225.

BALL: 1225. Did everybody get 1225? So, from the simplistic policy perspective, which you don't have to go too far to hear it, you would know something about the multiplication that you need to teach fourth graders. And what I'm about to show you is saying that teachers need to know multiplication-- which, of course, is right-- is barely skimming the surface. Now, how many of you have taught in this room? So, you know perfectly well that although you know the answer is 1,225, your students often won't, and they're going to produce other answers. And if all you know when you see the wrong answer is, oh, that's too bad, that's wrong, you're not in a very good position to do much, no more than a physician who can only tell you you're sick when you go into her office.

Here are three different answers to 49 times 25; and your task now isn't to show how you know how to do it, because I already know you know how to do it, but to see if you can figure out what mathematical steps produced these errors. You're not thinking about the student's thinking right now. You're not interviewing the student. Just how was the math done to produce this? Work with a partner or work on your own, whatever.

Okay, stop. How many people think they know what produced A? Raise your hand if you think you know what produced A. Look around and see how many hands are up. Okay. How many people think they know what produced be? What about C? Okay. Although I asked a moment ago how many of you have taught, the number of hands up is lower.

And, of course, I could give you more time to work on this, but not only does Phil deserve a chance to speak, but I'd like to make a point right now, which is, as a classroom teacher, you don't actually have 20 whole minutes to figure out why a student might have come up with something. Sometimes you do, of course. For example, you're sitting at home grading papers. You see that a whole bunch of students come up with 1,485. You might be able to spend a little time trying to figure out what in the world produced 1,485. But quite frequently, you're walking around the room and somebody produces a wrong answer, and it would be really good if you were fluent at being able to think of what might have produced that. And when you don't have that kind of fluency, your teaching is affected.

So an interesting piece of our work on content knowledge for teaching that we all need to worry more about is, is fluency mathematically when what you're doing is teaching math. You see, I'm giving you a little more time while I'm commenting on this. I can some of you still working on it. And it's a very interesting point that I'd like to sort of underscore, which is, we've gone to great pains in mathematics to underline the fact that being good at math doesn't mean being quick at it, and that is, of course, right. Good mathematicians spend years proving conjectures and revising theorems. And doing math isn't always quick.

I'm making a point about the math you do when you teach, which is often quick, on your feet, seizing an example, figuring out what a student might have done. And that is something worth our paying more attention to. For example, A, does somebody want to explain how A might have been produced?

AUDIENCE MEMBER: Yes. They multiplied 5 times 9 and got 45. They carried the 4, then added it into the 4; and then they multiplied 5 times 8 and got 40.

BALL: And on the second line?

AUDIENCE MEMBER: Then they multiplied 2 times 9 and got 18, and carried the 1, and added it into the 4; and 2 times 5 is 10.

[Applause]

BALL: There is at least one other possibility, although that's the one that's most likely. There is at least another. So if you have another, it's possible that could be too. But notice that having two possibilities would inform your ability to ask the student a good question next, or to pose an example to see what it is that's going on.

What about B?

AUDIENCE MEMBER: I think they multiplied 5 by 9 and got 45; then they carried the 4, and they multiplied 9 by 2; 18 plus 2 is 22, 225; and I think that carries through in the next one too.

AUDIENCE MEMBER: John is right. What he said is they went 9 times 25, and then 4 times 25, instead of 40 times 25.

BALL: Okay. And what about C?

AUDIENCE MEMBER: Well, this is the way I did it. I did 25 times 50, and subtracted 25. It looks like they did 25 times 50 and added it.

BALL: Why might that be? Why might somebody add rather than subtract? Anybody have an idea why might that happen?

AUDIENCE MEMBER: You're supposed to add ...(inaudible)

BALL: So you have a host of explanations of why that might happen. So, if you think that 49 is less, you might compensate by adding up. There are number of things you might consider. So this gives you some taste of the difference between what I showed you a moment ago, which is doing that, and doing the mathematical thinking you might have if you were teaching it.

The next example I would have used, but I'm going to leave it for you though if you don't download the slides, is to travel from being able to divide, 2 divided by two-thirds; to something you won't get to do right now but you can look it up, and that is looking at methods students have for dividing, 2 divided by two-thirds differently than the way you do it, and trying to figure out if the method a student uses actually would work for other fractions, or if it's just some nice event where the student gets the right answer, but using a method that would never work again; is it even a method?

And that's something that comes up a lot too. Students don't just get wrong answers, they get lots of right answers for reasons that look a little obscure if you have your own methods of doing things. And you have some responsibility to figure out should you put the kibosh on this; should you get the whole class to talk about it? What should you do? And if you don't have any idea if the thing will work in general, you're not in a very good position.

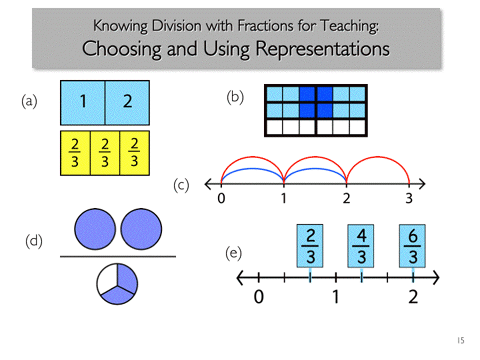
Another kind of work that we could try around the same question of two divided by two-thirds is, teachers often have to choose representations to try to illustrate a particular calculation. But they might make them up themselves, right. You might decide a drawing would really help. Well, that turns out to be more challenging than you think. But even if you're not so bold as to do that, your book will have diagrams in it, and you know what, the books will be wrong sometimes. Or sometimes they'll be correct, but require some real agility to make sure that the feature that's highlighted by the diagram is connected to the idea itself. And if you don't know how to do that, you're in bad shape. So another thing you could have tried would be to see which of these, in fact, is a reasonable-- can be reasonably interpreted to represent 2 divided by two-thirds.

But I'm going to go on to something a little harder, just so we don't stay only in kind of fourth/fifth grade content. Let's suppose that you wanted to teach students to simplify radicals. So I'd like you to start by simplifying this radical. This is again the case where, again, like in the other two examples, first, you just do the math; and then we'll try out what it would take if you were actually going to teach it. Don't forget, you can work with a partner.

Okay. What is the answer to this one?

AUDIENCE MEMBER: ...(inaudible)

BALL: Five times the square root of 6? Oh, some people are calculating ...(inaudible). So, again, I think it's worth remembering that teaching mathematics is not merely knowing mathematics in front of students. So the fact that you can calculate this is a nice start. It would be really irresponsible if you tried to teach people to simplify radicals without knowing how to do that. But suppose you wanted to engage kids in simplifying radical expressions; it might matter what examples you chose.

For example, what if you wanted to pick an example that would allow students to consider different solution paths for simplifying a radical. This we would call from our work, choosing numerical examples, which any of you who has taught knows that whether it's simplifying radicals, or dividing fractions, or teaching geometry, choosing the particular numerical or geometric examples matters enormously; and if you've ever been at the board, having picked an example not so skillfully, you know can happen. You say, oh, no, that's not the one I wanted.

What is that thinking that goes into picking an example carefully, so that what you want to come out is, in fact, what will get worked on? I'm not going to leave these up very long. I'll just give you a moment to consider, which of the following three radicals would be best if you wanted to set up a discussion among your students for alternative solutions paths for that? Or do you think it really makes no difference? It's possible they're all equally good. So take a moment to now go back, not just of what you would do, but what's involved in these? Does any of these set up a better discussion than any other?

Okay. Does anybody want to propose one or another of these?

AUDIENCE MEMBER: I propose A.

BALL: You propose A. Could you give your reasoning?

AUDIENCE MEMBER: ...(inaudible) out of that, which would be 9; so it would be the square root of 9 times 6; and then you can easily show then the square root of 9 is 3-- so the answer should be, 3 times the square root of 9.

BALL: So your reasoning is it would be relatively easy for them to do, is that right?

AUDIENCE MEMBER: You can show them an example that would be easy for them first and then get more complicated.

BALL: Okay. So there you see making visible his reasoning which was, he wants to think what will be sort of easy for them, because they should know this. But in fact, the question was slightly different. It's not that it's wrong. Actually, this is part of the work. What's the mathematical reasoning depending on what you want? And that mathematical reasoning fits his goal.

What if your goal is to have your students examine the fact that there are different solution paths for simplifying a radical? You might then choose 54. What would you choose?

AUDIENCE MEMBER: I would simply choose ...(inaudible)

BALL: Why?

AUDIENCE MEMBER: Given the fact that 2 is the only factor, you have the largest number of ways of viewing it, do you factor out the 4 first? Does the student see the 16 as a factor there? In B, there's really only one perfect square, and it's quite distinct from the other number that's a prime. And then A, you've got the confusion of you've got the third power through ...(inaudible) second. I think C is the most ...(inaudible)

BALL: So going into the insides of it like that, where it's not just about producing the answer, but thinking what comes up, and what would you be able to discuss with students, is a kind of mathematical reasoning important in teaching, and so is the answer that you gave. But that point about the difference between doing it and being able to think about it from the perspective of someone learning is different.

So I've given some examples analyzing student error as a task of teaching, considering-- and you really didn't get to do this one-- students coming up with non-standard but correct solutions. That's another kind of thing that can happen. We have to think, is this generalizable? Is it even a method? Choosing examples, is another; using representation, is another. And there are other kinds of work of teaching that we have in our research on teaching come to appreciate as being hugely mathematically intensive. And though they sound generic, as though they are kind of pedagogy, once you're inside trying to do them, they turn out to be mathematically complicated and require a kind of mathematical knowledge and reasoning not common necessarily to someone who is mathematically well educated for other purposes.

These are some of the examples of things that we have found very interesting that involve huge amounts of mathematical reasoning. For example, using and defining terms, it's great if you have in your university level courses, learned mathematically rigorous definitions. That's obviously pre-requisite and important. Most of those, however, are quite useless in trying to define terms at the fourth grade level. And what do you to then? Either you say, I'll use something approximate and then, inadvertently, you say things that are hugely inaccurate and cause confusion for students, or you're at a loss for how do you mediate between your own rigorous knowledge and what terms are available to students at that level that permit you to construct a mathematically precise but useable definition?

So, these are some of the examples that in our group we've become interested. And I want to highlight that as we've worked on this further, we've come to appreciate that what is often held separate, that is attention to diversity and equity and teaching mathematics are, in fact, not separate at all. Things like your choice of a context for a math problem needs on one hand to be absolutely appropriate for the mathematics and not distorted. But when that's all you do, you can very easily choose contexts that are create barriers for some of your students that are not part of their experience, that are either alienating or unfamiliar; and that, in fact, is an equity consideration that math teachers face everyday.

Well, what about language issues? Mathematics is a terrain in which language matters enormously. Some students in our classrooms are navigating not only between what we might call everyday language, and mathematical language, between home language, everyday school English, and academic mathematical language. And that transition across those language systems is one that has everything to do with who is and isn't learning mathematics in our classrooms, and demands a kind of level of mathematical skill much more than believing that equity matters. It's about knowing the math in a way that allows you to act on that commitment.

Now, you might ask at this point, so what are our hypotheses in our group about mathematical knowledge for teaching? So I want to go on to that at this point. Some of the common hypotheses that are out there are just quantitative. Teachers need to know some number of years beyond what they teach. And a phrase that's become very popular across our community is this phrase, pedagogical content knowledge. But in some of the review that Geoffrey Phelps and others in our group have done, we came to appreciate that that term is used in enormously different ways.

Certainly, between-- and you may not be aware of this-- between the mathematics education community and the science education community, that phrase means entirely different things in the literature, and we don't always realize that we're using a phrase that we've grown to appreciate because of its power to signify that knowing content for teaching isn't isomorphic with knowing content. And yet because it hasn't been well defined, we're actually talking past each other quite a bit of the time.

So I'd like to just say briefly how we now break out those ideas and why we're not repudiating in any sense pedagogical content knowledge, but how we think some distinctions within it will help.

We think that there's something called common content knowledge. By that we mean knowledge you'd expect reasonably well educated people to have. Like some of what you just did, like multiple 49 times 25. You'd like to think, although you can't always assume that, that many people who graduate from our school system would have what you would call a common level of mathematical knowledge. We know we aren't there yet as a society, but there is that sort of knowledge you might talk about.

Then there's a kind of specialized knowledge, and that's what you were exercising in my examples, where you have to think about the math in specialized ways because you're using it for teaching. Another would be a kind of amalgam of knowing about content and knowing things about kids, like what makes factoring numbers difficult for kids? Or what is involved in simplifying radicals that might be misconceptions for students? What kinds of things come up? That's kind of a mixture of knowing some particular things about a topic and how kids apprehend it.

And then, of course, there's what are ways to approach the teaching of a topic? What examples work well? What representations make the content transparent? So you might ask, well, what does any of that have to do then with the famous phrase, pedagogical content knowledge?

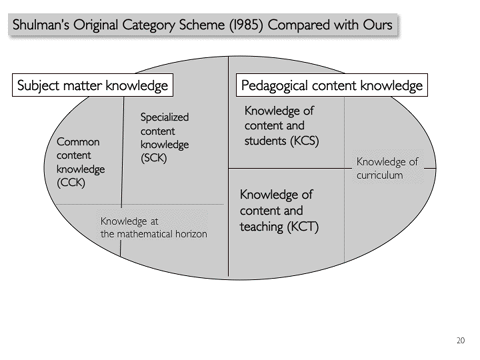
So we have a diagram that we found helps to portray how we're currently thinking about it that divides subject matter knowledge on the left from pedagogical content knowledge on the right. And inside of subject matter knowledge, we would list what I called common a moment ago, and specialized. In other words, it's knowledge of math. It's not about knowing about kids or how to teach it; it's just ways of knowing math. And on the right are these kinds of mixtures, knowing the content and how to teach it, and knowing how to ...(inaudible) kids. And recently as we've done more research in classrooms, studying videotapes and coding them, we're aware that there are some things bubbling up into this diagram that we'd like to pursue further, and we know many of you are interested in.

One is that there is certainly some knowledge of the curriculum. What happens when; and how do kids move through topics? If you're a mathematician, it's quite obscure how things are ordered and what that looks like as kids travel through it. And that's probably cutting through this knowledge of students and knowledge of content and teaching. And another that we would be remiss not to pay attention to is something that cuts across the content knowledge side of the diagram, which would be kind of like a knowledge of the horizon. Where do things go? What's the significance of a certain distinction in second grade that later on will turn out to have consequence in eighth grade?

If you don't have a sense of where things are going-- and here I don't mean the curriculum; I mean mathematical subtleties-- if you define even in odd numbers without attending to the fact that we're talking about whole numbers, you end up with weird things like kids thinking that 4.5 is even, because you haven't bothered to say that even numbers have to be whole numbers. So if you're not attentive to what will happen at the horizon, and only worry about where you're standing right now, that can be a problem. So these are areas we'd like to think more about.

Because of the time pressures today, I'm not going to talk a lot about developing and using that measure, which is what Joyce referred to. There's a reference to the fact that Heather Hill and I, and Geoffrey Phelps, and Laurie Sleep, and Mark Thames have been working on the survey measures-- Hyman Bass-- for a number of years. And I think Geoffrey is going to be talking about this, right, are you Geoffrey? Yes. And that will be an opportunity for people to learn more about it. And as I said, I'll post the slides so that you can learn more about what we are doing.

I think one result that I'd like to share before I sit down is to say that one use of this measures development, in addition to being helpful to those of you who run professional development projects and want to be able to evaluate whether those teachers in fact learn mathematics in these projects, which is a crucial point for us, is that it also allows us to test the validity of our claims. Is this knowledge that I've been talking about today, how do we know that it has anything to do with teaching better? And having measures allows us to ask that question and to begin to, as I said at the beginning, have some evidence about whether, in fact, we're even on the right track.

So, one of the analyses we were able to do as a function of having developed the survey measures is we were able to ask the question, if teachers score better on the survey measures, which measured the sorts of things I asked you to try a few minutes ago, do their students actually learn more? So, we built a measure using only about 30 items out of the survey items that we have created. It was a highly reliable measure. We were fortunate, because often it takes far more items than that to develop a reliable measure.

And then we built models in which we examined student gain scores using TerraNova, which was the measure in a study that we were conducting, which I won't talk about today. And we asked ourselves, what would predict student gains across a school year? I mean, we were interested in whether content knowledge would predict it, but there are lots of other things that predict student gains. For example, as the kid even in school, as the teacher there, what about the teacher's level of preparation? What about other things about all kinds of things? The family SES, for example, which in this country is a huge predictor of student learning? And that's the equity problem is it should not be the predictor of student gains, but unfortunately, it is.

And what we found was important, we thought. And that is that when compared with these other variables that we know play a role in predicting student achievement, we found that the teacher content knowledge measure was significant in predicting student gain scores. Now, if you translate the level of significance, we found that although it sounds low statistically, it's about equivalent as though two teachers who scored one standard deviation different on our measure, if their student's gains were compared, the students in the higher scoring teacher's classroom, it was as though they had received two to three weeks' more instruction in a year. So although the number may sound small, it helps to amplify what's meant by being significant. That's not trivial.

And perhaps even more interesting, the prediction from the content knowledge variable was about the same order of magnitude as the prediction of student family background variable. And that's probably even more important, and gives some hope to why investing in questions of teacher content knowledge may address not just the general problems of achievement in this country, but the enormous discrepancies and disparities in kids' opportunities to learn.

I'm going to stop at this point. I will, as I said, post the slides. In the slides, I also talk a bit more about the different things we've tried to test in our measures, what kinds of measures these are, and some results we've gotten from trying to investigate differences in professional development programs.

Let me just wrap up by saying that what we're trying to argue and what we've been working on is that content knowledge for teaching is different than that needed for other kinds of occupations. It's specialized to the work of teaching and it's content. And we shouldn't skip over it very lightly. We shouldn't go immediately to teaching approaches. And while that is important, this matters all by itself.

Second that there are many kinds of work that need to go into this. This is a problem that we share as a community. It's not the work of any one person, any one research group, or any single kind of work. We need multiple ways to tackle this question and to share measures, share ideas. Not somehow find millions of answers to this question. It's a pressing and important problem.

Items of the kind we've been writing, interestingly enough, turn out to be more credible to teachers than common tests. They recognize that the tasks as you tried are like the ones that they face in their classrooms. And finally, just to go back to where I began, I can't think of a problem that is more important than trying to figure out what seems on the surface simple. What does a teacher need to know about math in order to teach other people math? It's really a crucial question that's central to the improvement of our profession. Thank you.